In numerical computations, errors can propagate through calculations, potentially leading to significant inaccuracies in results. Understanding how errors propagate and how the conditioning of a problem affects numerical stability is crucial for designing robust numerical algorithms. In this post, I will discuss error propagation and the concept of conditioning in numerical problems.
Error Propagation
Errors in numerical computations arise from round-off errors, truncation errors, and uncertainties in input data. These errors can propagate through subsequent calculations, amplifying or dampening their effects depending on the nature of the problem and the algorithm used.
Types of Error Propagation
- Additive Propagation: When independent errors accumulate linearly through computations. For example, in summing a sequence of numbers, each with a small error, the total error grows proportionally.
- Multiplicative Propagation: When errors are scaled through multiplication, leading to potentially exponential growth in error magnitude.
- Differential Propagation: When small input errors lead to large output variations, particularly in functions with steep gradients.
Example of Error Propagation
Consider computing a function using finite differences: \(f'(x) \approx \frac{f(x+h) – f(x)}{h}\)
If \(f(x)\) is obtained from measurements with small uncertainty, then errors in \(f(x+h)\) and \(f(x)\) propagate through the division by \(h\), potentially amplifying inaccuracies when \(h\) is very small.
Conditioning of a Problem
The conditioning of a numerical problem refers to how sensitive its solution is to small changes in the input. A well-conditioned problem has solutions that change only slightly with small perturbations in the input, whereas an ill-conditioned problem exhibits large variations in output due to small input changes.
Measuring Conditioning: The Condition Number
For a function \(f(x)\), the condition number \(\kappa\) measures how small relative errors in the input propagate to relative errors in the output: \(\kappa = \left| \frac{x}{f(x)} \frac{df(x)}{dx} \right|\)
For matrix problems, the condition number is defined in terms of the matrix norm: \(\kappa(A) = \| A \| \cdot \| A^{-1} \|\)
A high condition number indicates an ill-conditioned problem where small errors in input can lead to large deviations in the solution.
Example of an Ill-Conditioned Problem
Solving a nearly singular system of linear equations: \(Ax = b\)
If the matrix \(A\) has a very large condition number, small perturbations in \(b\) or rounding errors can lead to vastly different solutions \(x\), making numerical methods unreliable.
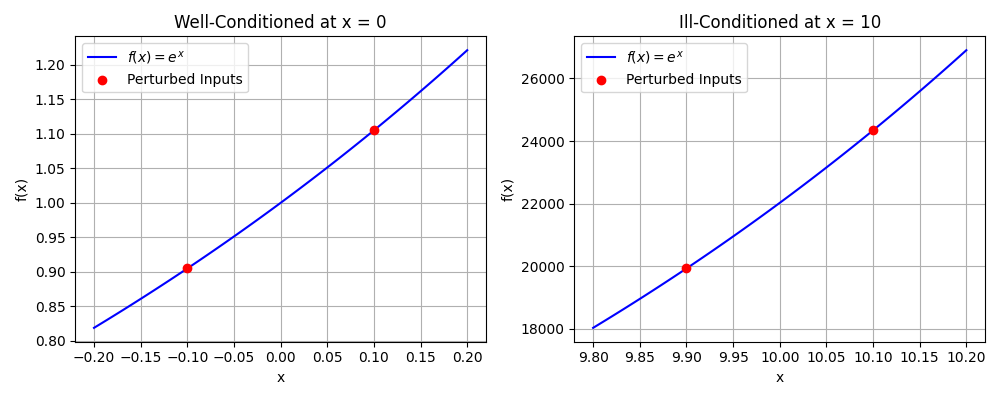
Visualizing Conditioning with a Function
To illustrate the concept of conditioning, consider the function \(f(x) = e^x\). The sensitivity of this function to input changes depends on the value of \(x\):
- Well-Conditioned at \(x = 0\): Small changes in \(x\) (e.g., \(x = -0.1\) to \(x = 0.1\)) lead to small changes in \(f(x)\), indicating a well-conditioned problem.
- Ill-Conditioned at \(x = 10\): Small changes in \(x\) (e.g., \(x = 9.9\) to \(x=10.1\)) cause large changes in \(f(x)\), illustrating an ill-conditioned problem.
The following figure visually demonstrates this concept, where small perturbations in the input lead to significantly different outputs in ill-conditioned cases while remaining controlled in well-conditioned ones.
Stability and Conditioning
While conditioning is an inherent property of a problem, stability refers to how well an algorithm handles errors. A stable algorithm minimizes error amplification even when solving an ill-conditioned problem.
Example of Algorithm Stability
For solving linear systems \(Ax = b\), Gaussian elimination with partial pivoting is more stable than straightforward Gaussian elimination, as it reduces the impact of round-off errors on ill-conditioned systems.
Conclusion
Understanding error propagation and problem conditioning is essential for reliable numerical computations. While some problems are inherently sensitive to input errors, choosing numerically stable algorithms helps mitigate these effects. In the next post, I will discuss techniques for controlling numerical errors and improving computational accuracy.
